特别说明：本文由学研汇技术中心原创撰写，旨在分享相关科研知识。因学识有限，难免有所疏漏和错误，请读者批判性阅读，也恳请大方之家批评指正。

原创丨彤心未泯（学研汇 技术中心）

编辑丨风云

层间激子，即束缚在两个单层范德华半导体上的电子-空穴对，具有良好的电调谐性和局部化性。由于此类激子显示出弱电子-空穴重叠，大多数研究仅通过光致发光检查了能量最低的激子。

近日，斯坦福大学Tony F. Heinz等人直接测量了层间激子的介电响应，使用它们的静电偶极矩来获取它们。继而确定了钨二硒化物\钼二硒化物异质结构中最低直接间隙层间激子的固有辐射寿命为0.40纳秒。作者发现电场和扭曲角的差异会导致激子跃迁强度和能量的变化趋势，这可能与波函数重叠、莫尔限制和原子重构有关。通过与光致发光光谱的比较，本研究确定了动量间接发射机制。对于依赖于光-物质相互作用的应用来说，吸收特性是关键。该成果发表在Science上。

介电函数是连接基本结构和设备功能的关键材料特性之一。它主要取决于材料中的电子能带结构和多体相互作用，对于光子和光电子应用的设计至关重要。在过渡金属二卤化物（TMDC）的二维半导体单分子膜（1L）中介电函数主要由与强束缚激子相关的电偶对相关的共振控制，这些电偶对是由这些材料中增强的库仑相互作用引起的。激子对介电函数的贡献通常通过反射对比度的吸收光谱ΔR/R来表征，同时通过光致发光（PL）测量，许多具有不同自旋和动量组态以及多激子态的激子物种已被识别，然而，这不允许确定材料的介电函数。

在TMDC异质双层膜中，两种不同的1L TMDC PL被用来研究层间激子（ILX），其电子和空穴成分位于相反的层。ILX显示出强大的电可调谐性和丰富的受限态，这些受限态源于周期势以及由moiré超晶格施加的周期势产生的丰富多样的受限状态，即晶格和扭曲角失配施加的两层之间空间变化的原子组态。由于它们的电子和空穴几乎没有波函数重叠，ILX的吸收很容易被大的层内吸收所掩盖，因此直接测定ILX的介电响应仍然是难以捉摸的。因此，关于ILX性质的许多含糊不清的问题一直存在，这对基本理解和它们在光学系统中的未来应用都很重要：比如它们的吸收强度、动量空间配置、固有辐射寿命，以及莫尔调制和重建的影响。

作者重点研究了H堆积（60°）异质双层膜，之前有报道称其具有多种ILX状态。WSe2/MoSe2异质双层封装在六角氮化硼（hBN）中，并配有背面和顶部石墨栅极（图1A）。通过向栅极施加一个适当平衡的正弦变化的偏置电压，在异质双分子层上感应一个交变电场F，电荷可以忽略不计。由于ILX的有限静电偶极矩p，其能量EILX经历了与样品中外加电场F成比例的调整：EILX=E0+pF。这反过来又导致了异质双分子层介电函数的调整，作者通过对使用锁定检测测量的单色光的反射率进行调整来记录。为了获得完整的光谱，在所需的光谱范围内调整探针波长。通过比较有调整和无调整情况下的反射率，并除以电场振幅，实验测定了反射率随电场的分数变化RF=(1/R)∂R/∂F。对于给定的激子共振，得到RF=(1/R)(∂R/∂EILX)p，其中通过收集不同dc值F的光谱来确定p。使用麦克斯韦方程组的解，将R及其导数∂R/∂EILX与介电函数ε联系起来，该解用转移矩阵实现，用于堆叠实验结构。同时注意到，由于ILX共振具有较小的振荡器强度，因此，∂R/∂EILX将其模型赋予RF，所以R没有被ILX共振有意义地修改。为了证实射频的起源是ILX共振中的场致位移，作者进一步测试了有意电荷调制的响应，没有发现可测量的信号。图1D显示了通过常规白光反射对比度测量获得的扭转角为60°±0.2°的样品从RF获得的ILX吸收光谱。RF和ΔR/R的相应基础测量如图1 B和C所示。这些结果产生的ILX振荡器强度比层内共振的强度小三到四个数量级。

在射频的低能区，可以观察到光子与光子之间18 meV的间隔特征。这些峰先前已在螺旋分辨和磁-PL光谱中观察到，并已分配给1s自旋反对齐 (a↑↓) 和自旋对齐 (a↑↑) ILX 跃迁，尽管PL测量也可以表现出动量间接跃迁。作者的数据证实了动量直接分配，因为动量间接激子的振子强度预计比直接跃迁弱得多，因此在吸收光谱中会弱可见。与PL测量不同，这里可以量化观察到的共振的振子强度。令人惊讶的是，自旋反取向峰的振子强度的力量是自旋取向峰的四分之一，在第二个H叠层样品中重现了类似的比率。这一发现与理论计算一致，并与1L TMDCs中自旋分裂激子的振荡强度差异大形成了鲜明的对比，这种区别可以理解为异质双层膜中沿平面外方向的镜像对称性破缺的结果。

进一步分析调制光谱揭示的一系列共振，使用直流电场依赖性来探索电子层和空穴层局部化。图1E显示了R_F与直流电场F_DC的演变。a↑↓峰和a↑↑峰的偶极矩分别为p↑↑= 6.2±0.6 e·Å和p↑↑=5.7±0.5 e·Å。这些值与电子态和空穴态的图像一致，电子态和空穴态的波函数位于相反的层中，与密度泛函理论（DFT）预测一致。作者还测量了第三个更高的能量峰值，用a_H表示（图1D），其电偶极矩较小为2.6±0.6 e·Å。然而，与低能ILX相比，这种高能ILX态预计具有较小的振子强度。因此，振荡器强度的增加和偶极矩的降低可以归因于这种高能态与MoSe₂ A激子A_Mo的混合。

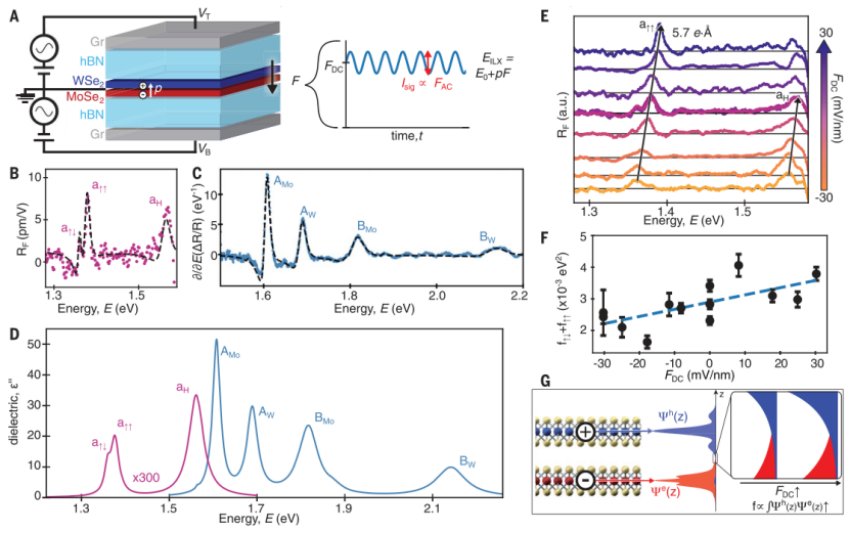
图 20 K下校准样品60°±0.2°的吸收光谱和电场依赖性

对于不同的样品自旋排列共振的能量一般随着扭转角的增加而增加（图2A）。为了解释能量转移，作者首先考虑了导电带和价带边缘之间的扭转相关动量失配的影响，如图2C所示。通过测量的电子、空穴和ILX有效质量可以计算出ILX带与光锥相交的能量。在MoSe₂中m_e=0.8m₀。在WSe₂中m_e=0.4m₀。然而，单凭这种效应并不能解释观测到的能量转移大小。因此进一步考虑了在空间上限制ILX并改变其频带色散的莫尔势的贡献。作者使用了一种连续哈密顿方法，其中势深度是一个拟合参数。对于120 meV的莫尔势阱深度作者预测了ILX跃迁能随扭转角的变化，这与实验数据是合理一致的。Δθ=56°和58°的电位V(r)分别如图2D和E所示并与图2G中相应的E_moiré叠加。尽管吸收测量比PL数据更能抵抗缺陷的影响，后者可能由低能量状态主导，但它们仍将受到可能的应变的影响。应变可以改变莫尔单元的能带能量和大小，这些因素有助于图2A所示实验数据的变化。关于过渡强度随扭转角度的变化，作者发现，如图2B所示，ILX振子强度随着晶体错位的增加而减少。因为吸收测量检查直接跃迁，不能简单地将这种效应归因于动量失配的增加，必须调用moiré模式的影响。这是通过两种不同的机制实现的：（i）层间距随着失调的增加而增加，从而减少电子-空穴波函数重叠和ILX振荡器强度。（ii）对于较小的莫尔周期，晶格重建的主导作用较小。在排列良好的H堆叠WSe₂/MoSe₂中这一结构有利于H_h^h原子结构，其具有最强的光学跃迁。对于排列不太整齐的样品，H_h^h区域覆盖了界面的较小部分，从而降低了整体过渡强度。仅第二种机制就可以解释ILX振荡器强度的大部分观察趋势，如图2B所示。

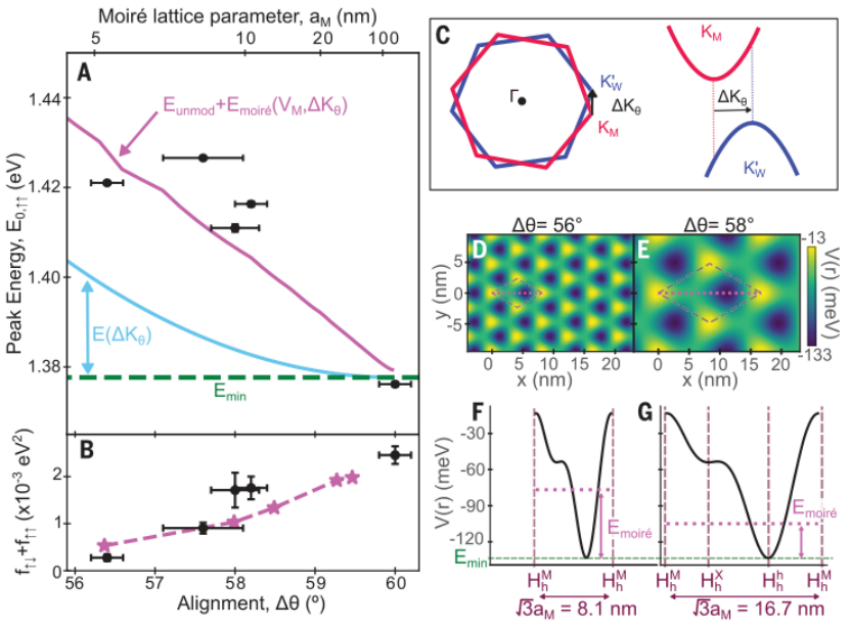
图 扭曲角度依赖性和莫尔波纹效应

最后，作者讨论了WSe₂/MoSe₂系统的ILX发射是由动量直接(K→K)跃迁还是由动量间接(K→Λ)跃迁主导的长期问题。在理论方面，作者计算了H_h^h晶格排列的能带结构和ILX吸收光谱，H_h^h晶格排列在排列良好的样品的莫尔单元中占主导地位。作者计算的GW能带结构预测，排列的异质双层的导带最小值位于L点（图3A）。相应地，使用GW-BSE形式计算的最低激发能主要由动量-间接电子-空穴跃迁K→Λ组成（图3B）。因为K→Λ跃迁是一个涉及声子的二阶过程，希望它出现在发射光谱中，但在吸收光谱中不可见。与动量间接激子和直接激子相关的预测静态偶极矩如图3C所示，将其与图3D中对齐良好的异质双层的实验测量的ILX静态偶极矩进行比较，其零场PL和吸收如图3E所示。作者发现吸收峰和PL峰的能量和偶极矩比值的计算结果与实验结果吻合较好，从而将吸收与K→K联系起来跃迁和PL到K→Λ跃迁。进一步支持这一识别的是测量ILX PL对激励功率和温度的依赖性（图3F和G）。这些研究揭示了一个更高的能量发射峰值L2的出现，该峰值与ILX吸收特征的能量相匹配，在高温和高激发功率下。热激活模型（图3G，插图）允许推断间接和直接之间的能量差。在低于L1特征的能量下，PL发射的宽肩归因于缺陷态或局部应变区，因为它在低功率下饱和，在高温下消失。总的来说，结果表明在排列良好的WSe₂/MoSe₂异质结构中，动量间接跃迁主导了ILX发射，但能量仅略低于吸收测量中看到的动量直接跃迁。因为K→Λ和K→K跃迁在能量上非常接近，它们在PL测量中的相对能量和优势在具有不同应变和扭转角的样品中有所不同。间接和直接ILX跃迁能量的相似性也解释了文献中K→K激子和K→Λ激子看似矛盾的断言。作者的测量允许从吸收光谱中提取的K→K ILX偶极矩与ILX PL之间的直接比较，从而避免了测量PL偶极矩绝对值时遇到的实验不确定性。

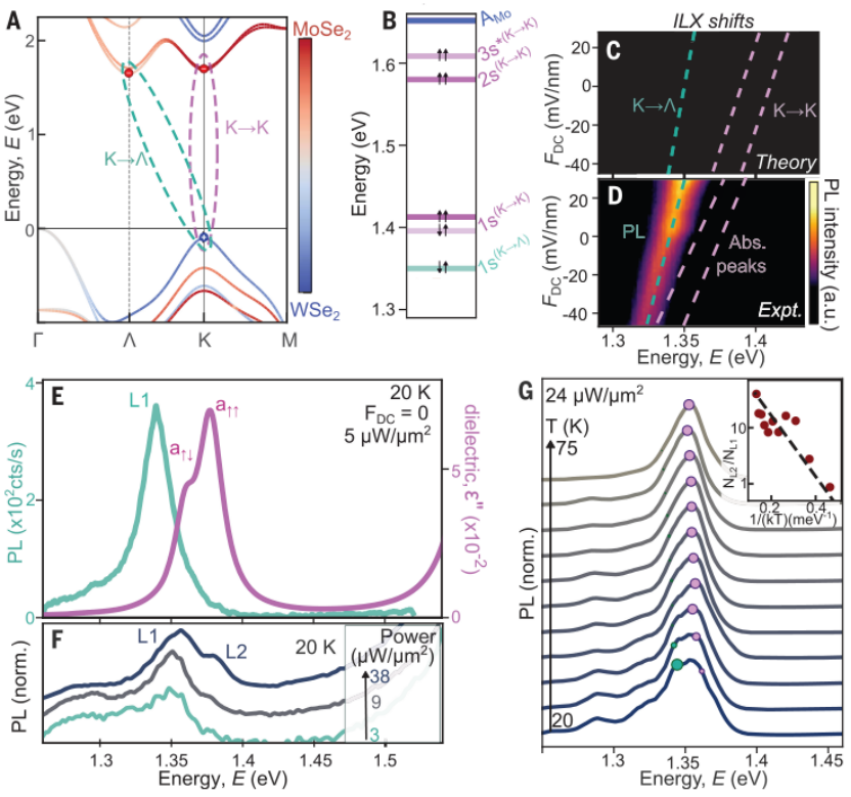
图  ILX光致发光的起源

除了为光致发光测量提供比较外，作者的电调制技术还允许直接测定ILX对介电函数的贡献。由此测得的振子强度确定的ILX辐射寿命不受非辐射过程的影响，而推断的跃迁能不受缺陷和局部化应变的影响，这些缺陷和局部化应变可以控制发射光谱。ILX辐射寿命和能量的稳健值使得能够探索扭曲角和莫尔势在WSe₂/MoSe₂系统中的作用。除了提供基本的理解，这些知识对于利用ILX的可调性和长寿命的光电器件中的异质双层系统的潜在应用是必不可少的。ILX介电响应的定量表征，再加上更长波长下ILX的发现，支持将这些材料集成到最先进的光子平台中的系统设计。

参考文献：

Tony F. Heinz et al. Optical absorption of interlayer excitons in transition-metal dichalcogenide heterostructures. Science, 2022, 376:406-410.

DOI: 10.1126/science.abm8511.

https://www.science.org/doi/10.1126/science.abm8511