特别说明:本文由学研汇技术中心原创撰写,旨在分享相关科研知识。因学识有限,难免有所疏漏和错误,请读者批判性阅读,也恳请大方之家批评指正。研究背景
量子霍尔效应揭示了由能带拓扑不变量分类的物质新相。量子霍尔边缘态的光学模拟开辟了一个新的研究领域,拓扑光子学,它在路由和产生电磁波方面带来了广泛的应用,如无背散射波导和拓扑绝缘体激光器。经典自由度通常用于在真实或合成维度中构建拓扑光模式。在经典拓扑之外,光固有的量子性质提供了丰富的根本不同的拓扑状态。
关键问题
拓扑光子学的研究主要利用光的经典属性,比如光的颜色、偏振和涡旋,“省略”了光的量子属性。光的量子属性会给拓扑物理带来什么影响仍不明确。与经典拓扑光子学中实维或合成维的模式格子相比,量子化光的拓扑态嵌入到Fock态Πini⟩晶格(FSL)中,FSL利用光的无限量子希尔伯特空间,使得仅用几个腔模式就能构建高维晶格。
新思路
有鉴于此,浙江大学王大伟、王浩华和宋超等人对超导电路中量子化光的拓扑态进行了实验,并由此构造了一维和二维的Fock态晶格,实现了丰富的拓扑物理,包括Su-Schrieffer-Heeger(SSH)模型的拓扑零能态、应变诱导的赝朗道能级、谷霍尔效应和霍尔丹手征边缘电流。本研究将光的拓扑状态扩展到量子领域,将凝聚态物理的拓扑相位与电路量子电动力学联系起来,并提供了控制多个谐振器的量子状态的自由。作者使用多个量子化的光模式来耦合原子,Fock态形成了SSH模型的1D和2D晶格,证明了拓扑零能态在1D SSH FSLs中的绝热输运,在2D FSLs中观察到了谷霍尔效应(VHE)和霍尔丹手征边缘电流。通过光子在R1和R2之间的振荡证实了拓扑边态的绝热输运,进一步通过量子态层析成像测量两个谐振器的密度矩阵表明了拓扑态的量子化。作者发现了VHE效应,并通过实验证明了这种效应。FSLs中的VHE可以用来相干传输两个谷之间的波函数,并控制多个谐振腔量子态的手征性。通过引入耦合强度的Floquet调制,作者综合了拓扑物理中的Haldane模型。在实验中,由于腔的退相干和非线性以及不完美的控制脉冲,手征旋转波函数向FSL中心移动。作者证明了拓扑零能态在1D和2D FSL中的相干控制,这些态只占据量子位子晶格,被真空拉比频率的一个能隙保护起来,不受其他本征态影响。将光的拓扑状态扩展到了量子系统,实现了凝聚态物理的拓扑阶段与电路量子电动力学相连接,提供了控制多个谐振器量子状态的自由。在这项研究中发展的技术也可以应用于控制FSL中的其他本征态,例如更高朗道能级中的激发态,且可推广到研究更复杂的量子谐振器耦合系统的拓扑状态。
技术细节
使用多个量子化的光模式来耦合原子。在两种光模式下,Fock态形成了SSH模型的一维(1D)晶格。通过仅仅增加一个其他模式,获得了二维(2D)应变蜂窝晶格,这些晶格的特征是依赖于位置的耦合强度。作者证明了拓扑零能态在1D SSH FSLs中的绝热输运,其中Fock态在叠加态中拓扑转移。在2D FSLs中,观察到了VHE和霍尔丹手征边缘电流,它们提供了一种设计多谐振器量子态的拓扑路线。利用电路QED平台有利的可集成性和可调谐性,设计并制造了一个超导电路来构建和设计FSL。
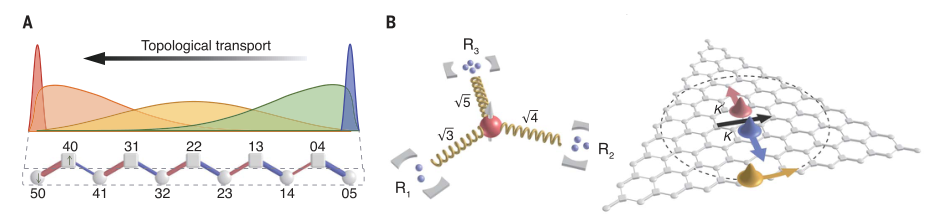
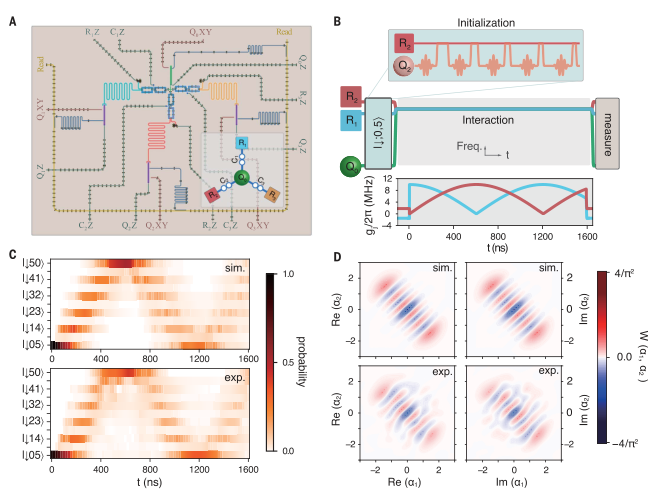
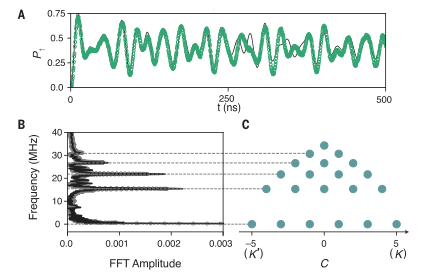
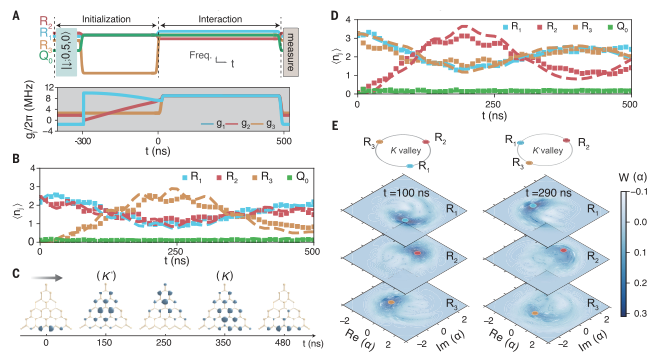
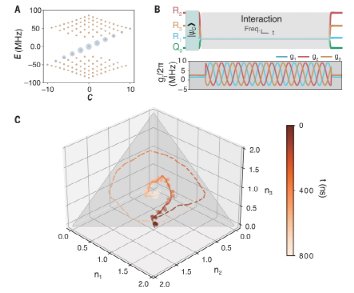
图 多模Jaynes-Cummings模型的Fock态晶格在实验中,选择R1和R2来构建SSH FSL,R3被远解谐并有效地与系统解耦。在实验脉冲序列中,我们首先准备SSH FSL的拓扑零能量状态,通过将五个光子经由Q2连续泵入R2。然后,调节参数以满足绝热条件。最后,测量了FSL中零能态的波包。光子在R1和R2之间的振荡证实了拓扑边态的绝热输运。零能态在拓扑上受到能隙g0的保护,不受FSL其它本征态的影响,并在输运过程中保持相干性。为了表明这一点,进一步通过量子态层析成像测量两个谐振器的密度矩阵。双模二项式态在两个谐振器的组合暗模中保持Fock态,并且从双模Wigner函数的负值可以明显看出态的量子化。图 焦点态Su-Schrieffer-Heeger模式下拓扑零能态的绝热输运作者形成了Fock态的二维蜂窝状晶格,依赖于位置的耦合强度引入了应变,当Q0与所有三个谐振器谐振时,该应变具有磁场的效应。通过分析晶格动力学的光谱来观察朗道能级。确定Q0的概率的演化,然后执行快速傅立叶变换,结果表明Lifshitz拓扑边缘将FSL分成半金属阶段和带状绝缘体两个阶段。通过引入线性势来模拟电场对电子的作用,可以观察到VHE,并通过实验证明了这种效应。量子位在演化过程中保持在基态,这反映了经典和量子预测之间的根本差异。FSLs中的VHE可以用来相干传输两个谷之间的波函数,并控制多个谐振腔量子态的手征性。通过引入耦合强度的Floquet调制,作者综合了拓扑物理中一个最重要的模型——Haldane模型。将平坦的Landau级转变为具有无间隙手性边缘态的双带结构,该结构源于Zeroth Landau级。实验中直接激发R1和R2得到一个初态。然后,周期性地调整耦合强度以实现霍尔丹哈密顿量。随后测量作为时间函数的平均光子数,显示了手征运动。理想情况下,波函数应该在内切圆上,即在Lifshitz拓扑边上。在实验中,由于腔的退相干和非线性以及不完美的控制脉冲,手征旋转波函数向FSL中心移动。
展望
总之,作者证明了拓扑零能态在1D和2D FSL中的相干控制。引入Floquet调制来实现了霍尔丹手征边缘电流。在这项研究中发展的技术也可以应用于控制FSL中的其他本征态,例如更高朗道能级中的激发态。该方法可以推广到研究更复杂的量子谐振器耦合系统的拓扑状态,其中谐振器的数量决定了FSL的维度,量子位的每个状态都标记了一个子晶格,其丰富程度超过了凝聚态物理中已知的拓扑相位。本研究为研究FSL中的拓扑相和发展玻色子模量子态工程的新控制方法铺平了道路。JINFENG DENG, et al. Observing the quantum topology of light. Science, 2022, 378(6623):DOI: 10.1126/science.ade6219.https://www.science.org/doi/10.1126/science.ade6219