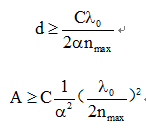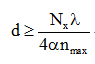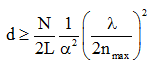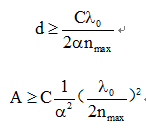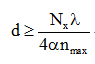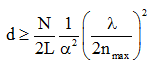特别说明:本文由学研汇技术中心原创撰写,旨在分享相关科研知识。因学识有限,难免有所疏漏和错误,请读者批判性阅读,也恳请大方之家批评指正。
光学系统在当今世界无处不在,从智能手机相机到显微镜和望远镜,都在捕获不断增加的数据并增强视觉感知。透镜等光学元件的减薄是近年来光学领域的重要目标。例如,创建轻薄的虚拟和增强现实耳机或夜视镜,将成为消费者和军事应用的游戏改变者。向小型化的推进需要更好的理论理解光学系统到底可以有多薄。
关键问题
复杂的光学元件设计可能需要长时间的计算,而且可能难以制造。这种复杂性也让人很难预测可能会发生什么。需要简单的极限来指导研究者进行设计,例如,需要的最小尺寸是多少?对于光学器件必须有多厚,甚至为什么光学器件从根本上可能需要厚度,人们一直缺少相应的基本认识。
新思路
有鉴于此,斯坦福大学David A. B. Miller等人研究表明了光学系统为什么以及何时需要厚度和宽度或面积。波衍射解释了在显微镜和照相机中,为了达到一定的分辨率或像素数,透镜或孔径的面积或直径的基本需求。这项工作表明,如果已知光学是做什么的,甚至在设计之前,也可以推断出所需的最小厚度。这个极限来自于衍射和重叠非定域性C概念的结合,这个概念可以严格地从器件的数学描述中推导出来。C表示不同输出区域的输入区域有多少重叠。这一限制广泛适用于光学,从相机到超表面,以及一般的波系统。
1、作者对成像系统进行了分析,定义了用于成像系统的ONL作者做了与成像系统相关的假设并进行了相关数学分析,基于分析过程定义了用于成像系统的ONL和C。2、分析获得了成像系统所需的厚度和面积以及最小厚度作者通过分析获得了光学系统横孔所需面积或厚度,并将其应用于成像仪获得了相关光学系统的最小厚度。作者分析了一般线性光学器件中的ONL,并构造了一般线性光学器件的矩阵。这些线性光学器件在输入和输出表面上具有连续的功能。作者演示了ONL在不同光学系统中的应用示例,包括像素化系统、连续系统、空间不变核的厚度,证实了该方法具有普适性。
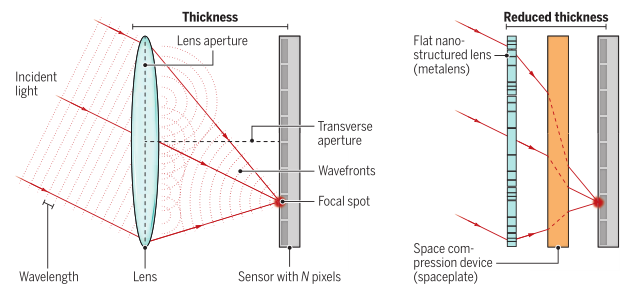
1、展示了光学系统为什么需要厚度,并推导出定量极限作者推导得出了光学系统最小可能厚度的定量限制,仅基于光学系统要执行的功能。在开始设计之前就可以推断出所需的最小厚度。本研究提供了一种理解系统最终会变得多么单薄的一般方法,作者分析应用于太空板,表明导出的极限是服从和接近现有设计的,还被用于确定成像系统以及进行模拟计算和图像处理操作的超表面所需的最小厚度。
技术细节
一个成像仪可能有一个透镜表面作为输入,一个像素传感器数组作为输出。作者做了以下几个假设:(1)成像仪是无损的;(2)互易光学——如果波可以向一个方向流动,那么它们的相位共轭可以以相同的透射因子向相反方向流动;(3)典型的成像仪,每个输出像素的输入功率基本上均匀地分布在输入表面。作者用数学方法将输入曲面和输出曲面平分为y-z平面上的曲面S考虑了输入曲面的右半部分和输出曲面的左半部分之间的映射,发现只有CRL=N/4个通道与将功率从输入平面的右半部分传输到输出平面的左半部分像素相关联。在此,作者定义了ONL和C。与分隔面S相关的ONL C是正交通道的数量C,这些正交通道必须从S一侧的输入交叉到S另一侧的输出,以实现所需的光学功能。假设所研究的光学系统是足够非局域的,它们需要这些C通道在连接输入和输出点的许多波长的横向距离上传播。因此,假设这些通道是传播电磁波。假设简单的局域电介质——在某一点上的极化仅仅取决于该点的场——所以忽略了等离子体激元或其他复合激发的非局域性。因此,可以使用波衍射启发式来预测尺寸限制。作者通过分析得到以下结果:
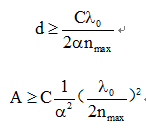
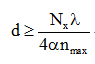
对于二维成像仪,有N个像素点,具有某些特征宽度或直径L,横向孔径面积为A~ Ld,则有:
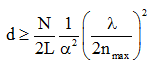
为了有效地利用横向孔径区域,需要将原本在x中的自由度交织到横向孔径中的它们的维度中,这可以设计超级耦合器来实现。然而,许多光学方法,包括自由空间传播、传统成像系统、简单介电堆结构和二维光子晶体,似乎不支持维度交错。在这种情况下,这些二维系统的厚度可能最终达到一维极限。将这些d的限制与成像仪和空间板的特定设计进行了比较,表明这些限制在现有的优化设计中是相近的。
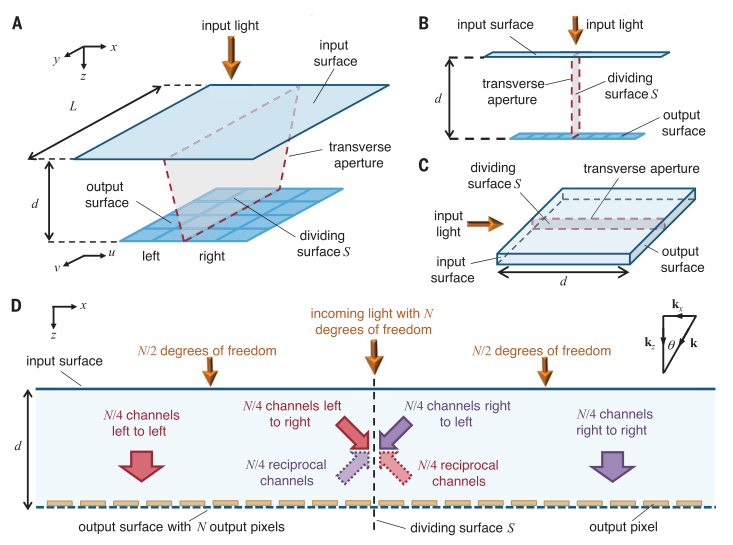
许多光学器件没有类似于成像仪的像素化,在输入和输出表面上具有连续的功能。因此,作者接着分析了一般线性光学器件中的ONL,构造了一般线性光学器件的矩阵。对于连续函数和/或没有像素化的函数,选择距离足够近的点——直观上足以表示函数中最小的凹凸。光学的SVD描述的经验与这种行为相当一致,算子紧凑性和相关的和规则保证了收敛性。
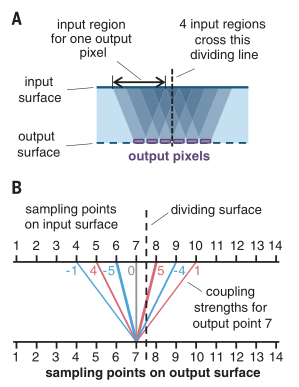
作者演示了ONL在不同光学系统中的应用,包括像素化系统、连续系统、空间不变核的厚度,作者详细地展示了ONL在上述系统中的计算过程,证实了该方法具有普适性。

展望
总之,作者通过各种例子在波的广泛情况下,包括像素、连续、空间变化和空间不变系统,表明有一个一般的方法来预测基本的最小所需厚度。经过优化设计的系统已经在一些小因子内接近这些极限。平面光学系统为系统厚度减薄提供了可能性,如通过使用超表面来消除透镜或其他元素的大部分厚度。这项工作表明,特别是对于具有大ONL的应用,尽管仍然需要总体厚度,但这个厚度中的大部分只需要横向传输光通道;它可能只需要是空的、均匀的或相对简单的波导空间,这将简化整个系统的设计。DAVID A. B. MILLER. Why optics needs thickness. SCIENCE, 2023, 379(6627): 41-45.DOI: 10.1126/science.ade3395https://www.science.org/doi/10.1126/science.ade3395FRANCESCO MONTICONE. Toward ultrathin optics. SCIENCE, 2023, 379(6627): 30-31.DOI: 10.1126/science.adf2197https://www.science.org/doi/10.1126/science.adf2197