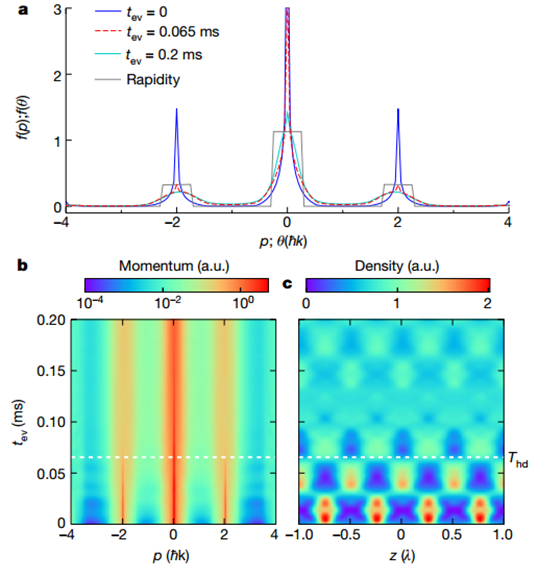
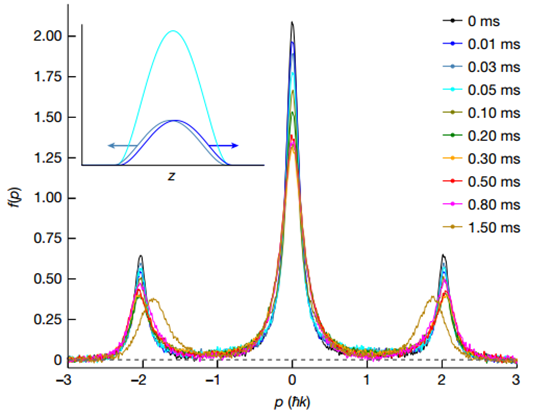
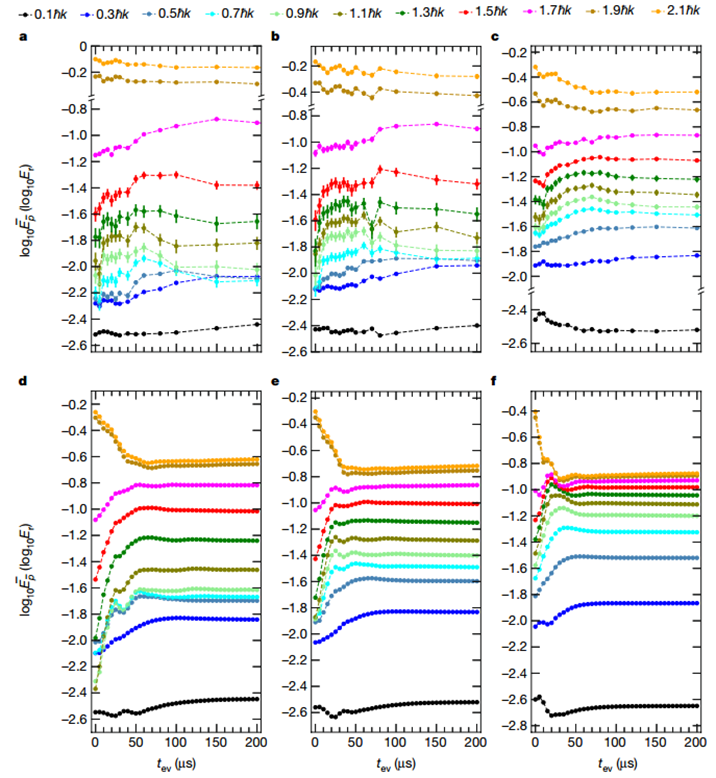
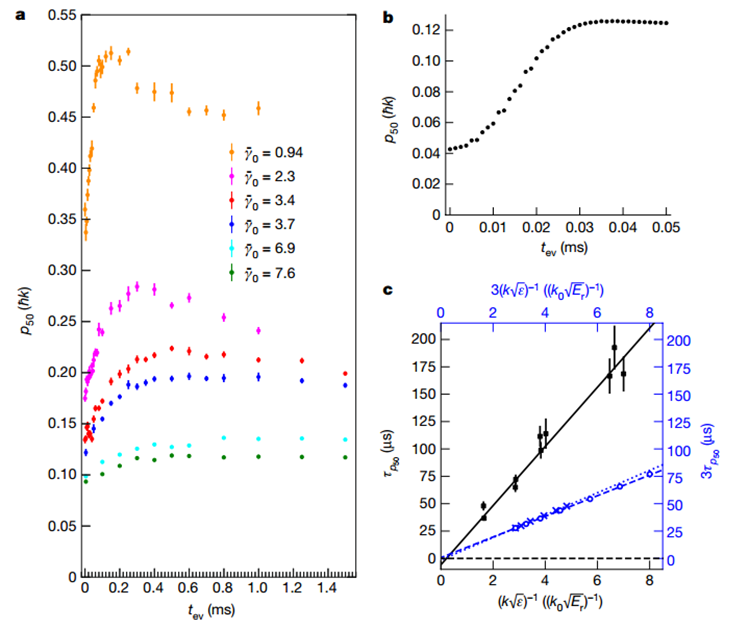
特别说明:本文由学研汇技术中心原创撰写,旨在分享相关科研知识。因学识有限,难免有所疏漏和错误,请读者批判性阅读,也恳请大方之家批评指正。在局部热平衡建立之前,流体动力学准确地描述了相对论重离子碰撞实验。这种在最快的可用时间尺度上发生的流体动力学出人意料的快速发生被称为流体动力学。当相互作用的量子系统以远大于其基态能量密度的能量密度淬灭时,就会发生这种情况。在流体动力学过程中,能量会在非常不同的能量尺度上重新分配。流体动力学先于动量模式之间的局部平衡,后者是近可积系统中广义吉布斯系综的局部预热化或不可积系统中的局部热化。尽管许多量子动力学理论假设局部预热化,但相关的时间尺度尚未通过实验研究。有鉴于此,宾夕法尼亚州立大学David S. Weiss等人使用一系列一维 Bose 气体来直接观察流体动力化和局部预热化。在应用布拉格散射脉冲后,流体动力化在远距离动量模式之间的能量快速重新分配中很明显,这发生在与布拉格峰值能量相关的时间尺度上。在附近动量模式之间的占用重新分配较慢中可以看到局部预热化。作者发现系统中局部预热化的时间尺度与所涉及的动量成反比。在流体动力化和局部预热化过程中,现有理论无法对实验进行定量建模。Tonks–Girardeau 极限中的精确理论计算显示出定性相似的特征。1)Tonks-Girardeau (TG)气体的流体动力学和局部预热化的物理学作者使用捕获的一维(1D)Bose 气体和点接触相互作用(Lieb-Lininger (LL)gas)观察流体动力学,并用布拉格脉冲淬火。与超冷气体的基态能量密度相比,脉冲赋予的高能量密度使得作者能够认识到这种普遍现象。捕获的LL气体的近可积性提供了一个框架,可以从中绘制适用于不可积系统的一般图景。由于1D Bose 气体的强耦合TG极限是完全可解的,作者详细解释了均质TG气体的流体动力学和局部预热化的物理学。实验从一束几乎零温度的一维气体开始,该气体由限制在蓝色失谐2D晶格中的 87Rb 原子组成,并由交叉的红色失谐偶极子俘获光束提供轴向俘获。作者在波矢k0 = 2π/(775 nm)的轴向晶格光束上脉冲6μs,然后测量动量分布作为脉冲后时间tev的函数,演示了不断发展的动量分布。流体动力化导致系统能量分布的快速变化。为了可视化这种变化,作者对连续动量范围内的动能进行积分,并将这些积分能量绘制为以反冲能量为单位的时间函数。正如预期的那样,速度分布不会在这些时间尺度上演变。TG-气体理论的各种流体动力学特征与相关实验中的相似。在具有相同快度能量的情况下,理论中的局部预热化速度是实验中速度的两倍以上。然而,由于曲线形状的多样性以及在此动量范围内流体动力学和局部预热时间尺度的适度分离,很难一致地提取局部预热时间常数。为了更好地研究局部预热化,关注动量模式之间的重新分配,这些模式的占用很大并且随动量迅速变化。作者在动量分界线pf中发现了一个强大的可观察到的,在中心峰中较低动量原子的f %和其余部分之间。通过找到p50处于其初始值和峰值之间一半的时间,从每条曲线中提取τp50。发现局部预热化p50的中点,p50m,与成正比。Le, Y., Zhang, Y., Gopalakrishnan, S.et al. Observation of hydrodynamization and local prethermalization in 1D Bose gases. Nature (2023).DOI:10.1038/s41586-023-05979-9https://doi.org/10.1038/s41586-023-05979-9