特别说明：本文由学研汇技术中心原创撰写，旨在分享相关科研知识。因学识有限，难免有所疏漏和错误，请读者批判性阅读，也恳请大方之家批评指正。

原创丨彤心未泯（学研汇 技术中心）

编辑丨风云

强相关系统中的几何阻挫可能会产生大量新颖的有序态和有趣的磁相，例如量子自旋液体。这种相的有前途的候选材料可以通过各向异性三角晶格上的哈伯德模型来描述，该模型捕捉了强相关性和磁阻挫之间的相互作用。然而，在存在流动掺杂剂的情况下，受挫磁性的命运以及它与方形哈伯德模型的掺杂相的联系仍不清楚。

有鉴于此，哈佛大学Markus Greiner等人研究了具有可控阻挫和掺杂的哈伯德模型的局部自旋顺序，使用各向异性光学晶格中的超冷费米子，从正方形到三角形几何形状连续可调。在半填充和强相互作用U/t ≈ 9 下，在单位点水平上观察到阻挫如何减少磁相关范围并驱动从共线Néel反铁磁体到短程相关120°螺旋相的转变。远离半填充时，三角极限显示出空穴掺杂侧的反铁磁相关性增强，并且在粒子掺杂超过 20% 时铁磁相关性反转，暗示了动磁在受挫系统中的作用。这项工作为探索三角晶格中可能的手性有序相或超导相以及实现t-t'方晶格哈伯德模型铺平了道路，这对于描述铜酸盐材料中的超导性可能至关重要。

系统设计

系统依赖于两束正交回射激光束干涉形成的晶格，其相对相位是主动稳定的。在相同的光束强度下，这种干涉实现了旋转45°的不可分离的方晶格。可调谐阻挫是通过沿着该方形晶格的一条对角线的额外隧道项t'引入的，并由两个光束之间的强度不平衡控制。

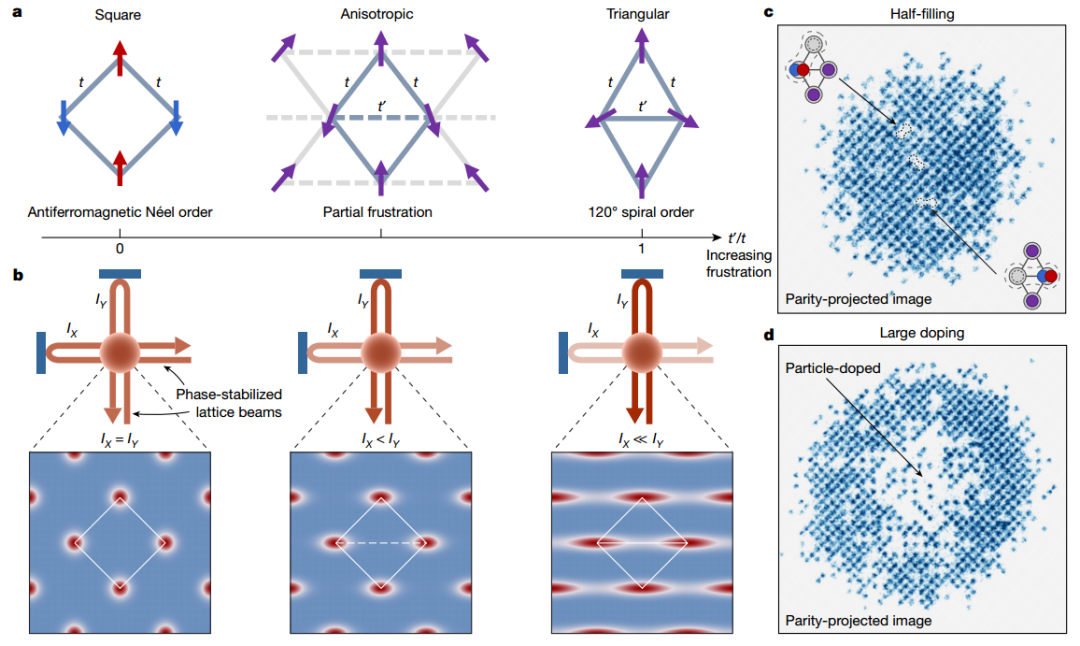
图  用量子气体显微镜研究可调谐三角晶格的阻挫

Néel 到螺旋阶跃迁

为了揭示各向异性三角形哈伯德模型在中间U/t下的磁特性，通过调整陷阱中心的局部化学势以大约达到半填充，形成了约500个原子的大型莫特绝缘体，并测量了位于位置r和r ± d的任意一对位点之间的自旋-自旋相关函数，观察到自旋-自旋相关性范围受到抑制。

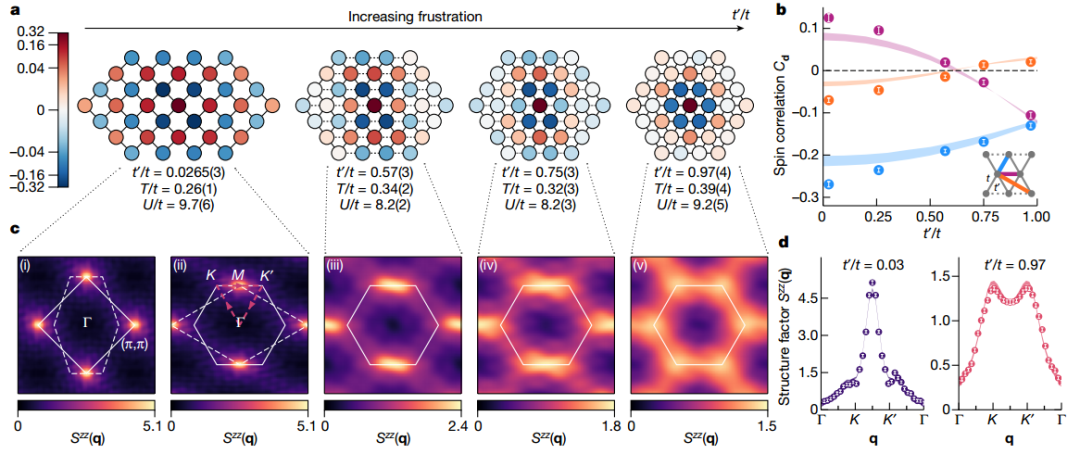
图  方形到三角形晶格转变中阻挫的短程反铁磁有序

粒子-空穴不对称性

通过将中心晶格填充增加到n = 1.6 来研究掺杂的影响，加上晶格限制导致的化学势的缓慢变化，实现了在局域密度近似中检查大范围的粒子和空穴掺杂 δ = n − 1的短程自旋相关性。在相同的温度下，反铁磁相关性在各种空穴掺杂中都存在，而反铁磁相关性则受到粒子掺杂的强烈抑制。

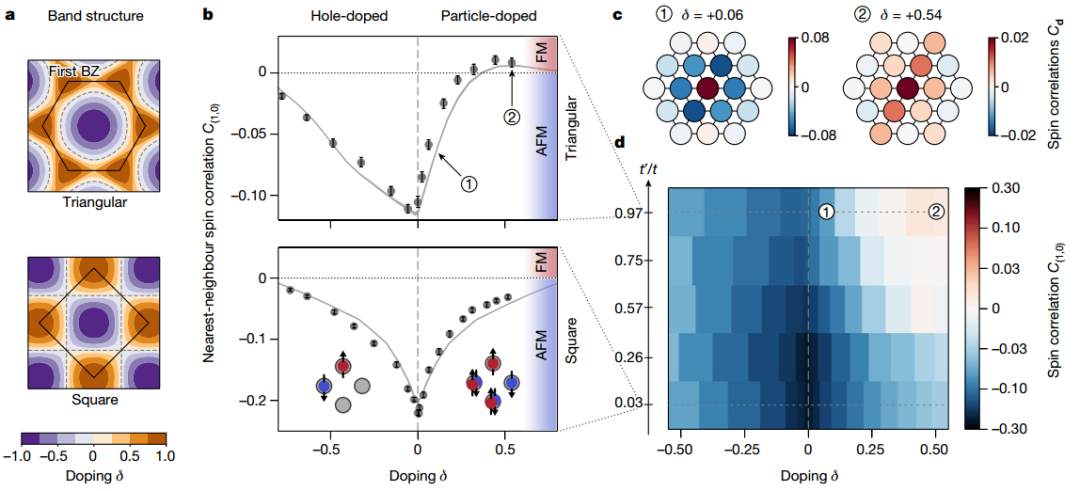
图  磁关联的粒子孔不对称性和粒子掺杂诱导的铁磁性

次近邻自旋相关性

粒子-空穴不对称性在沿对角键的自旋相关性中尤其明显。随着各向异性t′/t 的增加，对角键的性质从下一个最近邻变为最近邻，并且其值平滑地插值到三角形中的粒子-空穴非对称相关器。该相关器对粒子掺杂的铁磁特性在t'/t   0.5时最为明显。

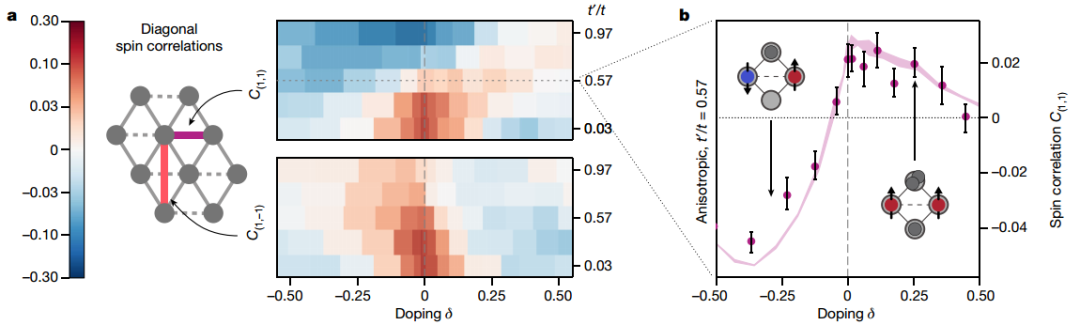
图  有限掺杂下的次近邻自旋相关性

参考文献：

Xu, M., Kendrick, L.H., Kale, A. et al. Frustration- and doping-induced magnetism in a Fermi–Hubbard simulator. Nature (2023). 

https://doi.org/10.1038/s41586-023-06280-5